Next: Dryrun: dryrun.f Up: Tranal utility Previous: Dielectric constant: diel.f Contents
This procedure computes time dependence of the mean square displacement (MSD) and evaluates the self-diffusion coefficient.
Input parameters for this utility follow after the trajectory parameters
in the NAMELIST block DIFF:
$DIFF parameter=value(s), ... $END
The following parameters are used:
FILDIF = <filename>
Defines the name of the output file
IDF = <int.num>
Defines the type of molecules for which diffusion is calculated
DTT = <value>
Defines the time interval (in 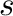 ) for MSD calculations. It is very recommended
that this parameter is equal to the time step of the trajectory multiplied
by
) for MSD calculations. It is very recommended
that this parameter is equal to the time step of the trajectory multiplied
by ISTEP parameter defined in the trajectory (TRAJ) section
of the input file. If the above requirement is not fulfilled, the program
may still work but less accurately.
NTT = <int.value>
Defines the number of steps for MSD calculation. The total time of tracking
the MSD will be thus DTT*NTT.
IAT = <int.value>
If IAT=0, MSD is calculated for the centers of masses of the selected
molecules. Otherwise MSD is calculated for IAT-th atom of each
molecule.
LCOM = <logical>
Specifies whether to correct for the total center-of-mass motion of the
selected molecules (that is, of type IDF). If .true., the
COM for each molecule is computed relative to center of mass motion of
the molecules of this type. The default is .false.. Note also, that
correction for the center of mass motion of the whole system is not
carried out (except the case of only one molecule type and
LCOM=.t.).
FBEG=<value>
Defines the beginning of linear fitting of the MSD curve to evaluate the
self-diffusion coefficient as: FBEG*DTT*NTT . The default value
is 0.2 , that is initial 20% of the MSD vs time dependense is not
included. It is always recommended to look at the computed MSD vs time
dependence to evaluate acceptable value for this parameter.
Futher comments
For each time 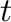 the MSD is computed as:
the MSD is computed as:
where averaging is taken over all molecules of type IDF and all
acceptable initial times 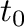 :
:
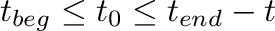 , where
, where
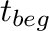 and
and 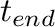 are the initial and final time of a continuous
part of the whole trajectory respectively. A trajectory is regarded as
continuous if each next configuration differ from the previous no more
than parameter
are the initial and final time of a continuous
part of the whole trajectory respectively. A trajectory is regarded as
continuous if each next configuration differ from the previous no more
than parameter BREAKM defined in the trajectory part (TRAJ)
of the input file.
The output file consists of the following columns:
The first column- time 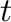 .
.
The second: for each 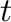 , evaluation of the diffusion coefficient as:
, evaluation of the diffusion coefficient as:
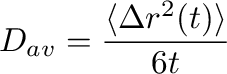
The third column: for each 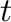 , evaluation of the diffusion coefficient as:
, evaluation of the diffusion coefficient as:
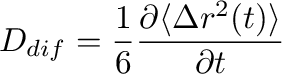
The 4-th column: root square of the MSD (average particle displacement)
5-th – 7-th columns: Evaluation of diffusion coefficient in X-, Y-, and Z-directions as:
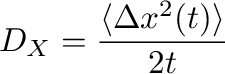
In all cases, diffusion is given in 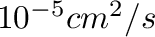 .
.