Next: Path Integral mode Up: The main input file Previous: Startup Contents
Expanded ensemble (EE) mode can be used for calculations of solvation free energies by gradual removal or insertion of molecules in the system. The theory and computational details behind the expanded ensemble method are described in papers (J.Chem.Phys.96, 1776 (1992); Molec.Simulations , 18, 43 (1996)). Details of the current implementation are described in Jämbeck et all, J.Comput.Chem.,34,187 (2013). Update 5.3.1 implements L2MC algorithm for Monte Carlo transitions between subensembles (Nikitin et al., J.Comp.Chem., 42, 787 (2021))
The expanded ensemble methodology implemented in MDynaMix from v.5.2.3,
includes the Wang-Landau algorithm,
Wang F., Landau D. P., Phys. Rev. Lett. 86, P. 2050–2053 (2001)),
for optimization of the balancing factors. Also, from v.5.2.5,
a different scheme of interaction change of the choosen solute molecule
with the rest of the system, based of soft core interaction potentials
(see e.g. L.Luder, R.Kjellander, J.Phys.Chem.B., 110, 15514 (2006)) ,
is implemented. Particularly, the interaction potentials
between all pairs of the solute and solvent atoms are changed with the insertion
parameter 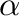 ,
,
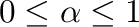 according to:
according to:
The coupling parameter 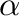 assumes a number of fixed values between
0 and 1, where “1” corresponds to the solute molecule properly inserted
in the solvent, while value “0” correspons to the fully eliminated
solute (which then can be considered as an a gas phase). The program computes
probability distribution over subensembles with different values of
assumes a number of fixed values between
0 and 1, where “1” corresponds to the solute molecule properly inserted
in the solvent, while value “0” correspons to the fully eliminated
solute (which then can be considered as an a gas phase). The program computes
probability distribution over subensembles with different values of 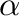 ,
from which the free energy difference can be obtained. Additional bias for
transition probabilities between subensembles is given by the
balancing factors (biased potential over the insertion parameter), which need
to be tuned in order to provide reasonable
homogenious distribution of probabilities over subensembles. The Wang-Landau
procedure is by default used for tuning of the balancing factors, but there
is also possibility for manual tuning.
,
from which the free energy difference can be obtained. Additional bias for
transition probabilities between subensembles is given by the
balancing factors (biased potential over the insertion parameter), which need
to be tuned in order to provide reasonable
homogenious distribution of probabilities over subensembles. The Wang-Landau
procedure is by default used for tuning of the balancing factors, but there
is also possibility for manual tuning.
Note: Special care should be taken in MDEE simulations of molecules having zero Lennard-Jones potential for hydrogen atoms (like SPC or TIP3P water). Simulation may become unstable when repulsive potential between oxygens becoms weeker while electrostatic attraction between hydrogen and oxygen still present. It is advisable to prescribe some small Lennard-Jones potential to such hydrogens.
The expanded ensemble is specified by the following keywords:
MDEE <num_ensembles> <mode>
Run expanded ensemble simulations with <num_ensembles> subensembles,
Parameter <mode> can be one of:
manual : manual setup of EE parameters, that is 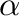 -points
and balancing factors which remain fixed during the simulation
-points
and balancing factors which remain fixed during the simulation
WL : balancing factors are optimized during the simulation according to
Wang-Landau algorithm (J.Comp.Chem., 34, 187 (2013))
auto: 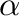 poins are set with equal separation between them
within the [0:1] interval, balancing factors are tuned automatically by
the Wang-Landau algorithm.
poins are set with equal separation between them
within the [0:1] interval, balancing factors are tuned automatically by
the Wang-Landau algorithm.
L2MC : In addition to “auto” option, L2MC algorithm for transitions between
subensembles is used (Nikitin et al, J.Comp.Chem., 42, 787 (2021))
In the case parameter mode is not set to auto or L2MC, the MDEE
command should be followed by exactly num_ensembles lines,
with two number on each: the value of coupling parameter 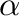 and
balancing factor, corresponding to this subensemble. Values of balancing
factors are given per inserted molecule in units of “
and
balancing factor, corresponding to this subensemble. Values of balancing
factors are given per inserted molecule in units of “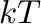 ”.
”.
In the case of automatic setup of the expanded ensemble parameters,
the set of coupling parameters 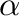 is choosen uniformly in the range [0:1]
(that is,
is choosen uniformly in the range [0:1]
(that is,
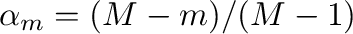 where
where 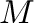 is the total number of
subensembles
is the total number of
subensembles <num_ensembles>.
Default mode: auto
EE_typ <i_typ>
Specifies that the molecules of type i_typ are those which are
inserted/deleted in the EE procedure.
This keyword is required!
In the case of automatic optimization of the balancing factors (mode
auto, WL, L2MC), additional keywords can be used:
Num_pass <value>
Defines how many times the system should walk between the extreme subemsembles and back in order to complete one WL iteration. Default is 2.
Num_WL <value>
Defines the number of WL iterations. After this number of WL iterations is carried out, the optimization of balancing factors is completed, and the program proceeds with EE procedure with fixed balancing factors. Default is 10 iteration.
WL_parameters <increment> <factor>
Sets up initial increment in the Wang-Landau optimization of balancing factors, and scaling factor by which the increment is scaled after each WL iteration.
Default values: increment = 0.1, factor = 0.5.
In case of automatic WL tuning of the balancing factors (mode auto)
the program starts expanded ensemble simulation with zero balancing factors.
In case of mode WL the initial values of the balancing factors are
introduced from the input. After each attempt of visiting
a subensemble, an increment is added to the corresponding balancing factor.
After walking between extreme subensembles at least Num_pass times,
a WL series (sweep) finishes and the value of the increment is decreased by
a factor (default value 0.5, see keyword WL_parameters).
Notes:
1. If WL procedure has not performed necessary number of iterations
(keyword Num_WL), the program gives warning in the output
“Expanded ensemble simulation not converged yet”. Then the computed
free energy values may not be accurate or not relevant at all.
It is always recommended to continue simulation long enough after the
balancing factors are optimized.
2. While evaluating results, ensure that the system has walked at least several times between the extreme subensembles (the first and the last). Look at the “table of transition” in the end of the output.
3. Pay attention at the acceptance ratios for transitions between subensembles, they can be found in the last two columns of the section “Distribution over subensembles” in the output. The acceptance ratios should not be too low. If they are too low (a few percent or less), the number of subensembles should be increased.
EE_start-in <start_in>
Start EE simulation in subensemble number <start_in>.
Default: in the last subensemble (that is, with completely deleted
EE molecule(s))
EE_freq <steps>
Try EE transition after steps MD steps.
Default: 10
EE_new
Change balancing factors after restart (manual mode only). Otherwise the old values written in the restart file are used.
EE_offset <b-value>
Value of parameter 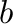 in equation (12)
in equation (12)
Default: 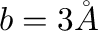 .
.
EE_power <w1> <w2>
Values of parameters 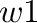 and
and 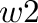 in equation (12)
in equation (12)
Default: 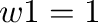 ;
; 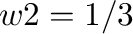 .
.
Probability_threshold <P_low>
Assing value P_low to computed subensembles probabilities which
are lower than this number
Default: 0.001